Link
Introduction
부제: 우리가 수학을 배워야 하는 이유
대학에서 물리학을 배우던 시절 나는 같은 학과 학부생들 중에 수학을 제일 못해 친구들의 도움을 많이 받았었다.
가시적으로 무언가 진전이 보이는 것이 아닌 논리만으로 모든 것이 맞물리는 수학의 세계를 이해하기엔 내 머리가 그만큼 좋지 않았던 것 같다.
사람은 자신이 잘하는 것이 있으면 그것에 더 관심을 갖게 되고 더 많은 시간을 할애하며, 익숙하지 분야에까지 자신이 잘하는 분야의 방법을 적용하는 등 사고방식에까지 영향을 주며 고착화되는 경향이 있다.
수학을 못했기에 논리보다는 그 수들의 연산을 행할 때 어떤 일이 일어나는지를 상상하는데 더 많은 관심을 쏟기 시작했고, 다른 사람들과는 다른 독특한 방식으로 수를 다루기 시작했다.
하지만 그건 어디까지나 제대로 된 수학은 아니여서 진짜 수학을 못해 벽에 부딪히는 경우가 많았다.
예를 들면 이번 문제의 경우, n이 작기 때문에 실제로 “UUUUU”까지 만들어보다가 주어진 단어와 같아지는 순간 정답을 반환해도 최대 3905번의 연산만 하면 되기 때문에 시간초과는 안난다.
하지만 만약 “UUUUUUUUUUUUUUUUU”가 몇 번째 단어인지를 찾는다면?
38,146,972,655번의 연산을 해야한다. 당연히 시간초과다. 하지만, 수학을 적용하면 순식간에 문제를 해결할 수 있다.
수학이라는 건 이미 논리적으로 검증된 사실들을 굳이 체크하지 않고 건너뛰는 마치 메모이제이션과 같은 도구라는 생각이 든다.
아, 그래서 난 어떻게 했냐고?
Note
- 글자가 5개 미만이라면 A를 붙이고, U에서 한 글자 더 올릴 때 다음 글자가 똑같이 U라면 해당 글자를 W로 치환해둔다.
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
WORD_TABLE = "AEIOU"
def change_up(ch):
return WORD_TABLE[WORD_TABLE.index(ch) + 1]
def carry_over(word):
word_list = list(word)
for i in range(len(word_list)-1, -1, -1):
cur_ch, prev_ch = word_list[i], word_list[i-1]
if cur_ch == 'W':
if prev_ch == 'U':
word_list[i-1] = 'W'
else:
word_list[i-1] = change_up(prev_ch)
return ''.join(filter(lambda w: w != 'W', word_list))
def solution(word):
w, answer = 'A', 1
while w != word:
if len(w) < 5:
w += 'A'
elif w[-1] != 'U':
w = w[:-1] + change_up(w[-1])
elif w[-1] == 'U':
w = w[:-1] + 'W'
w = carry_over(w)
answer += 1
return answer
풀이
1. 필요한 함수 정의
한 번 직접 만들어보자. 그러려면 어떤 행동이 필요할까?
- 단어의 뒤에 A를 붙이는 것
- 글자를 한 단계씩 올리는 것 (A -> E)
- 단어를 올림하는 것 (AAAAU -> AAAE)
1번은 그냥 하면 될 것 같고, 2, 3번을 구현해야 할 것 같으니 정의 해보자
1
2
3
4
5
6
7
8
9
def change_up(ch):
pass
def carry(word):
pass
def solution(word):
answer = 0
return answer
2. 원하는 단어가 될 때까지 변환
우선 첫 번째 글자를 A로 준다.
1
2
3
4
5
6
7
8
9
def change_up(ch):
pass
def carry_over(word):
pass
def solution(word):
w, answer = 'A', 1
return answer
취할 행동을 위에서 언급한 대로 3가지이다.
- 글자가 5개 미만이라면 뒤에
A를 붙인다. - 마지막 글자가
U가 아니라면 마지막 글자를 한 단계 올린다. - 마지막 글자가
U라면 해당 글자를W로 치환하고 그 글자를 올림한다.
이걸 내가 가진 단어가 주어진 단어와 같아질 때까지 반복한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def change_up(ch):
pass
def carry_over(word):
pass
def solution(word):
w, answer = 'A', 1
while w != word:
if len(w) < 5: # 2-1
w += 'A'
elif w[-1] != 'U': # 2-2
w = w[:-1] + change_up(w[-1])
elif w[-1] == 'U': # 2-3
w = w[:-1] + 'W'
w = carry_over(w)
answer += 1
return answer
3. 함수 구현
우선 파라미터로 받은 문자를 한 단계 올려주는 change_up()부터 살펴보자.
이건 간단하다. 테이블을 하나 만들어 두고 받은 문자의 다음 인덱스의 문자를 반환하면 된다.
1
2
3
4
WORD_TABLE = "AEIOU"
def change_up(ch): # 3-1
return WORD_TABLE[WORD_TABLE.index(ch) + 1]
다음으로 단어의 문자들을 올림하는 함수를 구현해보자.
우선 사용 상의 편의를 위해 문자열(string)을 리스트로 만들고, 순회를 할건데 가장 마지막 인덱스에서부터 0번째 인덱스까지 역순으로 순회를 한다.
i번째의 문자가 current_character이고, i-1번째의 문자가 previous_character이다.
1
2
3
4
def carry_over(word):
word_list = list(word)
for i in range(len(word_list)-1, -1, -1): # 3-2
cur_ch, prev_ch = word_list[i], word_list[i-1]
체크할 것은 아래와 같다.
- 현재 문자가 W인가?
- 맞으면, 앞의 문자가 U인가?
- 맞으면, 그 문자를 W로 바꾼다.
- 아니면, 그 문자를 한 단계 올린다.
- 아니면, pass
- 맞으면, 앞의 문자가 U인가?
1
2
3
4
5
6
7
8
9
def carry_over(word):
word_list = list(word)
for i in range(len(word_list)-1, -1, -1):
cur_ch, prev_ch = word_list[i], word_list[i-1]
if cur_ch == 'W': # 3-3
if prev_ch == 'U':
word_list[i-1] = 'W'
else:
word_list[i-1] = change_up(prev_ch)
이제 이 단어 리스트에서 남아 있는 W는 올림처리를 다 해줬기 때문에 필요 없으므로 걸러내주고 문자열로 바꿔 반환한다.
1
2
3
4
5
6
7
8
9
10
def carry_over(word):
word_list = list(word)
for i in range(len(word_list)-1, -1, -1):
cur_ch, prev_ch = word_list[i], word_list[i-1]
if cur_ch == 'W': # 3-3
if prev_ch == 'U':
word_list[i-1] = 'W'
else:
word_list[i-1] = change_up(prev_ch)
return ''.join(filter(lambda w: w != 'W', word_list))
번외. 수학을 적용한 풀이
1
2
3
4
5
6
7
8
9
WORD_TABLE = "AEIOU"
def solution(word):
answer, r = 0, 5
for i, w in enumerate(word):
a = WORD_TABLE.index(w)
n = r - i
answer += a * ((r ** n - 1) / (r - 1)) + 1
return answer
정리 안 하려고 하다가 그건 좀 아닌 것 같아서 업데이트 했다.
컴퓨터가 노가다를 해준 결과 이런 규칙을 발견할 수 있었다. 왼쪽에 채워진 A들은 무시하고 가장 오른쪽 알파벳만 보자
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
5번째 자리 - 1씩 증가
AAAAA: 5
AAAAE: 6
AAAAI: 7
...
4번쨰 자리 - 6씩 증가 (1 + 5)
AAAA: 4
AAAE: 10
AAAI: 16
...
3번째 자리 - 31씩 증가 (6 + 25)
AAA 3
AAE 34
AAI 65
...
2번째 자리 - 156씩 증가 (31 + 125)
AA 2
AE 158
AI 314
...
1번째 자리 - 781씩 증가 (156 + 625)
A 1
E 782
I 1563
5번째 자릿수 부터 역순으로 증가치를 나열해보자
1, 6, 31, 156, 781, …
근데 이건 그냥 딱 봐도 등비수열이다.
1
2
3
4
5
A1 1 = 1
A2 6 = 1 + 1*5^1
A3 31 = 1 + 1*5^1 + 1*5^2
A4 156 = 1 + 1*5^1 + 1*5^2 + 1*5^3
A5 781 = 1 + 1*5^1 + 1*5^2 + 1*5^3 + 1*5^4
이므로, 일반항 An은 아래와 같다.
1
2
a = 1, r = 5 일 때,
An = a + r^(n-1)
각각의 증가치는 등비수열의 합이다. 등비수열의 합 공식은 아래와 같다.
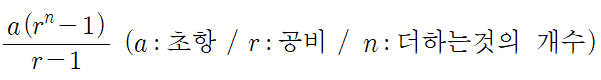
시험 삼아 A5만 구해보자.
1
1 * ((5^5)-1) / (5-1) = 781
문제 없는 것 같으니 예시를 하나 생각해보자
EIO는 1189라고 한다. 이 숫자는 어떻게 구해진 걸까? 여기서도 등비수열의 합 공식을 사용한다.
1
2
3
4
5
6
7
8
1번째 자릿수에서 숫자를 하나 바꾸는 데는 781만큼 숫자가 더해진다.
E는 A->E로 1번 바꾸므로 781,
2번째 자릿수에서 숫자를 하나 바꾸는 데는 156만큼 숫자가 더해진다.
I는 A->E->I로 2번 바꾸므로 312,
3번째 자릿수에서 숫자를 하나 바꾸는 데는 31만큼 숫자가 더해진다.
O는 A->E->I->O로 3번 바꾸므로 93
정리하자면, 자릿수별로 등비수열의 합을 구한 다음에 아래의 인덱스를 곱해주면 된다.
1
2
01234
AEIOU
다 더하면 1186이다. 음? 뭔가 이상한데? 다른 숫자로도 계산을 해보니 자릿수의 갯수 만큼 숫자가 빈다.

이유는 알파벳이 바뀌고 바로 다음 자리수에 바로 알파벳이 차는게 아니라 공백부터 시작하기 때문에 시작점이 언제나 -1 된 상태에서 더해나가기 때문이다. (실제로 AAAA에서 5개 만큼 더하면 AAAE가 아니라 AAAAU가 된다.)
이건 그냥 더할 때마다 값을 1씩 더해주면 된다.
그럼 이걸 코드로 옮겨보자. 근데 n을 그대로 쓰려고 보니까 역순으로 되어 있어서 좀 헷갈린다. n을 우리에게 친숙한 인덱스 i를 사용해서 바꿔 써주자
n = r - i
1
2
3
4
5
6
7
8
9
WORD_TABLE = "AEIOU"
def solution(word):
answer, r = 0, 5
for i, w in enumerate(word):
a = WORD_TABLE.index(w)
n = r - i
answer += a * ((r ** n - 1) / (r - 1)) + 1
return answer
광기 (지금 생각하고 있는 그거 맞다)
Comment
수학을 적용한 풀이는 안 정리하고 넘어갈까 하다가 정리했는데 생각보다 시간이 많이 걸렸다;;
하지만 수학의 중요성을 다시금 되새기기 위해서라도 정리했어야 됐으니까 뭐…괜찮나?
