Link: https://leetcode.com/problems/trapping-rain-water/
Introduction
그냥 우연히 펼친 파이썬 알고리즘 인터뷰 책에 전에 혼자서는 못 풀고 책에 있는 풀이의 도움을 받아 풀었던 문제가 있어서 다시 풀어보니 기억이 잘 안나서(제대로 이해를 못 했다는 뜻) 정리하게 됐다.
Solution
I. 문제 정의
n의 최대치가 20,000이기 때문에 O(n^2)으로 풀면 수행횟수가 4억이 되어버리기 때문에 무조건 시간초과가 난다.
따라서 그보다는 적은 시간내에 풀 수 있는 방식으로 접근해야 한다.
II. 투 포인터

left와 right 두 개의 포인터를 두고 left는 오른쪽으로, right는 왼쪽으로 진행시키면서 쌓인 물의 높이를 더해나간다.
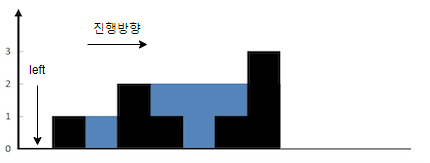
우선, left 포인터를 기준으로 생각해보자. 편의상 가장 높은 기둥의 오른쪽까지는 날려버리고, left가 체크하는 범위는 시작점 부터 가장 높은 기둥까지로 제한한다. 그 오른쪽 부분은 right 포인터가 체크할 것이다.

웅덩이 부분에 들어왔을 때부터 나갈 때까지는 오른쪽에 항상 left가 지나온 기둥보다는 더 높은 기둥이 존재할 것이다.
그렇기 때문에 물 웅덩이가 쌓을 수 있는 물의 양은 둘러 싸고 있는 왼쪽 오른쪽 기둥 중 더 작은 높이인 왼쪽의 기둥의 높이 - 현재 위치이다.
우선 여기까지를 코드로 구현해보자. water는 물 웅덩이의 양이고, left와 right 포인터를 지정해준다.
1
2
3
4
class Solution:
def trap(self, height: List[int]) -> int:
water = 0 # 1
left, right = 0, len(height) - 1 # 1
right는 신경쓰지 말고 left만 움직여보자.
1
2
3
4
5
6
7
class Solution:
def trap(self, height: List[int]) -> int:
water = 0
left, right = 0, len(height) - 1
while left < right:
left += 1 # 2
left가 지나오면서 가장 높았던 기둥의 높이를 기억해두자.
1
2
3
4
5
6
7
8
9
class Solution:
def trap(self, height: List[int]) -> int:
water = 0
left, right = 0, len(height) - 1
left_max = 0
while left < right:
left_max = max(left_max, height[left]) # 3
left += 1
전술했듯이, 어차피 오른쪽은 더 높은 기둥으로 막혀 있어서 왼쪽 기둥의 높이와 현재 높이 만큼의 차이가 쌓인 물의 양이다.
1
2
3
4
5
6
7
8
9
10
11
class Solution:
def trap(self, height: List[int]) -> int:
water = 0
left, right = 0, len(height) - 1
left_max = 0
while left < right:
left_max = max(left_max, height[left])
water += left_max - height[left] # 4
left += 1
이걸 right도 똑같이 반복한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
def trap(self, height: List[int]) -> int:
water = 0
left, right = 0, len(height) - 1
left_max, right_max = 0, 0
while left < right:
left_max, right_max = max(left_max, height[left]), max(right_max, height[right])
water += left_max - height[left]
left += 1
water += right_max - height[right] # 5
right -= 1
여기서 똑같이 한 번에 한 칸씩 움직이게 될 경우 한 포인터가 먼저 가장 높은 곳에 도착하게 되면 그 포인터는 더 이상 앞으로 움직이면 안되기에 제한 조건을 걸어줘야한다.
한 번에 똑같이 한 칸씩이 아니라 더 낮은 위치에 있는 포인터를 먼저 움직이면서 진행시키면 한 쪽이 가장 높은 기둥에 도착했을 때부터는 다른쪽 포인터가 도착할때까지 기다리게 할 수 있다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
def trap(self, height: List[int]) -> int:
water = 0
left, right = 0, len(height) - 1
left_max, right_max = 0, 0
while left < right:
left_max, right_max = max(left_max, height[left]), max(right_max, height[right])
if height[left] < height[right]: # 6
water += left_max - height[left]
left += 1
else:
water += right_max - height[right]
right -= 1
return water
이 알고리즘의 시간복잡도는 O(n)이고, 공간복잡도는 O(1)이다.
Comment
Stack을 사용하는 방법이 있는데 아무리 봐도 도저히 이해가 안되서 이해가 되면 다시 이 포스팅을 업데이트 해야겠다. 근데 Stack 방법보다는 이 포인터 방식이 더 직관적이고 마음에 든다.
