Link
Introduction
뭔가 복잡해 보이지만 의외로 가상으로 대회를 해보면 간단하게 풀리는 문제이다.
Note
- 두 사람의 거리(번호의 차이)가 1이라고 하더라도 대결을 하지 않는 경우가 있으므로 주의
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import math
def to_next_round(order):
return math.ceil(order/2)
def solution(n,a,b):
matching_round = 1
while n > 1:
if abs(a-b) == 1 and to_next_round(a) == to_next_round(b):
break
n //= 2
matching_round += 1
a = to_next_round(a)
b = to_next_round(b)
return matching_round
1. 1명만 남을 때까지 대결
1라운드 부터 시작해서 n명의 참가자가 1명이 남을 때까지 무작위로 상대를 골라 대결을 진행해보자. 토너먼트이기 때문에 대결이 진행될 때마다 참가자는 절반씩 줄어든다.
1
2
3
4
5
def solution(n,a,b):
matching_round = 1
while n > 1: # 1-1
n //= 2
matching_round += 1
이번엔 무작위로 하지 말고, 문제에 써져 있는 것처럼 이긴 사람을 다시 번호를 매겨서 앞 사람과 대결하게 하자.
여기서 규칙을 한 번 살펴보자.
1
2
3
4
5
6
7
8
9
1번이 이기면 다음 번호는? 1번
2번이 이기면 다음 번호는? 1번
3번이 이기면 다음 번호는? 2번
4번이 이기면 다음 번호는? 2번
5번이 이기면 다음 번호는? 3번
6번이 이기면 다음 번호는? 3번
...
다음 라운드의 번호를 얻는 규칙은 현재 번호를 2로 나누고 반올림 한 숫자가 다음 라운드의 번호가 된다.
1
2
3
4
5
6
7
8
9
10
11
12
import math
def to_next_round(order):
return math.ceil(order/2)
def solution(n,a,b):
matching_round = 1
while n > 1:
n //= 2
matching_round += 1
a = to_next_round(a) # 1-2
b = to_next_round(b) # 1-2
2. A가 B를 만났을 때
현재 대결을 하는 사람과의 특징은 번호가 1만큼 차이가 난다는 것이다. (1번과 2번, 3번과 4번)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import math
def to_next_round(order):
return math.ceil(order/2)
def solution(n,a,b):
matching_round = 1
while n > 1:
if abs(a-b) == 1: # 2-1
break
n //= 2
matching_round += 1
a = to_next_round(a)
b = to_next_round(b)
하지만 여기서 또 고려해줘야 할 것이 있다. 예를 들어, 2번과 3번의 경우 대결을 하지 않지만 번호 차이가 1인데, 두 사람이 대결을 하는지 어떤지는 어떻게 알 수 있을까?
대결 후 무조건 이긴다고 가정했을 때 두 사람이 다음 라운드에서 같은 번호를 가지고 있으면 된다.
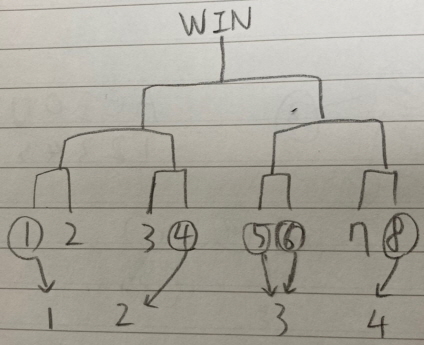4번과 5번은 번호 차이가 1이지만 대결하지 않는다
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import math
def to_next_round(order):
return math.ceil(order/2)
def solution(n,a,b):
matching_round = 1
while n > 1:
if abs(a-b) == 1 and to_next_round(a) == to_next_round(b): # 2-2
break
n //= 2
matching_round += 1
a = to_next_round(a)
b = to_next_round(b)
return matching_round
Comment
처음 이 문제를 접했을 때 엄청 복잡한 문제일거라 생각하고 지레 겁을 먹었던 기억이 난다.
이 문제를 일반 수학 문제처럼 나 혼자 풀어야 하는게 아니라 컴퓨터랑 같이 푼다는 사실이 정말 다행인지도 모르겠다. 나는 상황을 주고 가상 세계에서 실제로 실험해보면 되니까.