Sliding Window

Introduction

Sliding Window 알고리즘을 처음 접한게 언제였는지 기억이 안나지만 조금 헷갈리기 시작해 시간을 들여 정리해두면 다신 안 까먹겠지 싶어서 포스팅을 하게 됐다.

LeetCode 문제를 풀다 보면 연습유형으로 굉장히 많이 보게 되는 단어가 있다.

median(중간값), subset, subtree, subarray, …

그 중에서도 subarray의 부분배열의 합에 대한 문제는 Sliding Window 알고리즘을 사용하기에 제격인데, 아주 명확하게 풀이가 된 곳(https://www.geeksforgeeks.org/find-subarray-with-given-sum/)이 있어서 참고하면서 정리해봤다.

Brute Force

아래와 같은 상황을 생각해보자.

• Input: arr = [1, 4, 20, 3, 10, 5], sum = 33
• Output: 부분배열의 합 중 가장 길이가 긴 배열. 없을 경우 -1을 반환

n(arr의 길이)이 한 1000 이하라면 아래와 같이 모든 부분 배열을 다 체크하는 풀이로 간단하게 끝낼 수 있을 것이다.

# Brute Force [O(n^2)]
def solution(arr, sum_):
    answer = [-1]
    for i in range(len(arr)):
        for j in range(i+1, len(arr)):
            if sum(arr[i:j]) == sum_:
                answer.append(arr[i:j])
    return sorted(answer, key=len)[-1]

n이 1000 이하일 경우 O(n^2)이니까 1,000,000번의 수행으로 끝나서 시간초과는 안날테지만 그 이상의 경우 더 짧은 시간 안에 해결해야 한다.

여기서 사용되는 게 Sliding Window 알고리즘이다.

Sliding Window

나는 사실 슬라이딩 윈도우라고 하는 이름을 듣고 이 알고리즘이 어떻게 동작하는지 바로 떠올리기가 어려웠다. 오히려 이걸 앞뒤가 자유자재로 늘어나는 지렁이 한 마리가 배열 위를 기어가는걸 연상했다.

슬라이딩 지렁이 윈도우 알고리즘에서는 포인터를 2개(left, right) 두고 이 포인터를 움직이면서 포인터 안에 있는 배열을 체크하며 앞으로 나아간다.

더 많은 부분 배열을 포함할 수 있을 것 같다 싶으면 머리(right)가 전진하고, 부분 배열의 합이 특정 값을 넘을 경우 꼬리(left) 한 칸씩 줄어들어 부분 배열의 값을 줄이며 부분 배열의 합을 체크하는 방식이다.

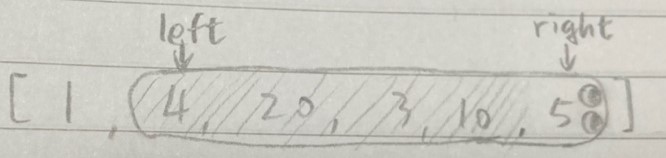이런 느낌…

Solution

1, 우선 필요한 변수들을 준비해 둔다. 지렁이의 머리가 인덱스 1부터 시작하므로 현재 부분 배열의 합에는 배열의 첫번째 값을 미리 넣어 놓는다.

def solution2(arr, sum_):
    answer = [-1]
    cur_sum, n = arr[0], len(arr)
    left, right = 0, 1

2, 지렁이 머리를 끝까지 움직이면서 계속 더해 나간다.

def solution2(arr, sum_):
    answer = [-1]
    cur_sum, n = arr[0], len(arr)
    left, right = 0, 1

    while right <= n: #2
        if right < n:
            cur_sum += arr[right]
        right += 1

3, 더하다가 혹시라도 합이 원하는 수치와 일치하면 정답 리스트에 넣는다.

def solution2(arr, sum_):
    answer = [-1]
    cur_sum, n = arr[0], len(arr)
    left, right = 0, 1

    while right <= n:
        if cur_sum == sum_: #3
            answer.append(arr[left:right])

        if right < n:
            cur_sum += arr[right]
        right += 1

4, right가 전진하다보면 필요 이상으로 더할 때가 있다. 부분 배열의 합이 sum_보다 높아지는 경우인데, 이 때는 left가 right의 바로 이전 위치로 올 때까지 체크하면서 기존에 구해뒀던 부분 합에서 하나씩 빼준다.

def solution2(arr, sum_):
    answer = [-1]
    cur_sum, n = arr[0], len(arr)
    left, right = 0, 1

    while right <= n:
        while cur_sum > sum_ and left < right - 1: #4
            cur_sum -= arr[left]
            left += 1

        if cur_sum == sum_:
            answer.append(arr[left:right])

        if right < n:
            cur_sum += arr[right]
        right += 1

5, 이 과정을 끝낸 후 정답 리스트를 길이 순으로 정렬하고 가장 마지막(가장 긴 길이의) 부분배열을 반환하면 된다.

# Sliding Window [O(n)]
def solution2(arr, sum_):
    answer = [-1]
    cur_sum, n = arr[0], len(arr)
    left, right = 0, 1

    while right <= n:
        while cur_sum > sum_ and left < right - 1:
            cur_sum -= arr[left]
            left += 1

        if cur_sum == sum_:
            answer.append(arr[left:right])

        if right < n:
            cur_sum += arr[right]
        right += 1

    return sorted(answer, key=len)[-1] #5

처음에는 어떻게 한 방향으로만 전진만 하는데 빠지는 것 없이 모든 유효한 부분 배열을 체크할 수 있을까 하는 의구심이 들었는데, 그림을 그리고 손가락으로 포인터를 가리키며 이것저것 해보다 보니 이해가 됐다.

• 부분 합이 초과될 때마다 지렁이의 머리는 멈추고 꼬리는 앞으로 움직인다.
• 꼬리가 멈춰서는 지점에서의 부분배열의 합은 언제나 sum_보다 낮거나 같고 이러한 매 지점을 체크포인트로 하여 그 앞의 배열들을 체크해 나가기 때문에 가능성이 있는(부분배열의 합이 낮거나 같은) 배열들은 모두 체크를 할 수 있다.

References

• https://www.geeksforgeeks.org/find-subarray-with-given-sum/