Link
Introduction
쿼드 트리 압축이라는걸 이번 문제를 풀면서 처음 알게 되었는데, 뭔가 예전에 학교 수학시간에 배웠었던 어떤 그림이 떠오른다.
 이런거
이런거
재귀함수에 대해서 모르는 사람이라도 문제를 재귀적으로 해결하면 되겠다고 감각적으로 알 수 있는 문제이다.
우리가 테트리스 게임을 처음 해보더라도 어떤식으로 플레이할지 바로 알 수 있듯이 그냥 문제 자체가 보자마자 알 수 있는 THE 재귀문제 라는 느낌.
다만 이걸 어떻게 구현할지에 대해서 조금 머릿속이 복잡해져서 살짝 헤매긴 했지만 귀찮다라고 느꼈지 어렵다라고 느끼진 않은 문제였다.
Note
- 압축 가능한지 체크 하고 분할하는게 더 효율적이다.
- 분할 시에 고정된 좌표와 움직이는 좌표를 구분하며 구현한다.
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def count_zero_and_one(arr, x1, y1, x2, y2):
result = [0, 0]
for y in range(y1, y2):
for x in range(x1, x2):
result[arr[y][x]] += 1
return result
def check_if_compressible(arr, x1, y1, x2, y2):
zero, one = count_zero_and_one(arr, x1, y1, x2, y2)
n = (x2 - x1) * (y2 - y1)
return zero == n or one == n
def split(x1, y1, x2, y2):
MID_X, MID_Y = x1 + (x2 - x1) // 2, y1 + (y2 - y1) // 2
areas = [
[x1, y1, MID_X, MID_Y],
[MID_X, y1, x2, MID_Y],
[x1, MID_Y, MID_X, y2],
[MID_X, MID_Y, x2, y2]
]
return areas
def f(arr, x1, y1, x2, y2):
result = [0, 0]
compressible = check_if_compressible(arr, x1, y1, x2, y2)
if compressible:
result[arr[y1][x1]] += 1
return result
areas = split(x1, y1, x2, y2)
for area in areas:
zero, one = f(arr, *area)
result[0] += zero
result[1] += one
return result
def solution(arr):
return f(arr, 0, 0, len(arr), len(arr))
1. 필요한 함수들 정의
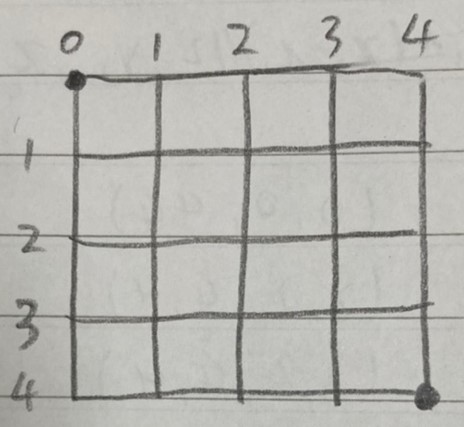
여기 이 4X4 사각형에서 점이 찍힌 두 좌표 (x1, y1) = (0, 0)와 (x2, y2) = (4,4) 사이에 있는 사각형들을 체크해나갈건데, 필요한 행동을 3가지 정도로 정리해봤다.
- 사각형 안의 숫자들을 전부 센다.
- 사각형 안의 숫자들이 압축 가능한지 판별한다.
- 사각형을 4분할로 나눈다.
1
2
3
4
5
6
7
8
9
10
11
12
def count_zero_and_one(arr, x1, y1, x2, y2):
pass
def check_if_compressible(arr, x1, y1, x2, y2):
pass
def split(x1, y1, x2, y2):
pass
def solution(arr):
answer = []
return answer
그리고 어떻게 구성될지는 모르겠지만 배열과 사각형의 범위를 넣어주면 그 범위 안에서 압축도 알아서 하고 아무튼 숫자를 다 체크해서 반환해주는 마법의 함수 f()를 정의한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def count_zero_and_one(arr, x1, y1, x2, y2):
pass
def check_if_compressible(arr, x1, y1, x2, y2):
pass
def split(x1, y1, x2, y2):
pass
def f(arr, x1, x2, y1, y2):
pass
def solution(arr):
return f(arr, 0, 0, len(arr), len(arr))
2. 숫자를 세는 함수 구현
result 리스트에서 0번째 인덱스에는 0의 개수, 1번째 인덱스에는 1의 개수 이므로 해당 좌표의 값을 인덱스로 해서 개수를 하나씩 세면 깔끔한 코딩이 가능하다.
1
2
3
4
5
6
def count_zero_and_one(arr, x1, y1, x2, y2): # 2
result = [0, 0]
for y in range(y1, y2):
for x in range(x1, x2):
result[arr[y][x]] += 1
return result
3. 사각형이 압축가능한지 판별
좌표 범위 안에 있는 n개의 사각형과 0의 개수 혹은 1의 개수가 완벽하게 똑같으면 압축이 가능하다.
1
2
3
4
def check_if_compressible(arr, x1, y1, x2, y2): # 3
zero, one = count_zero_and_one(arr, x1, y1, x2, y2)
n = (x2 - x1) * (y2 - y1)
return zero == n or one == n
4. 분할
4X4 정사각형을 실제로 분할해서 생각해보자
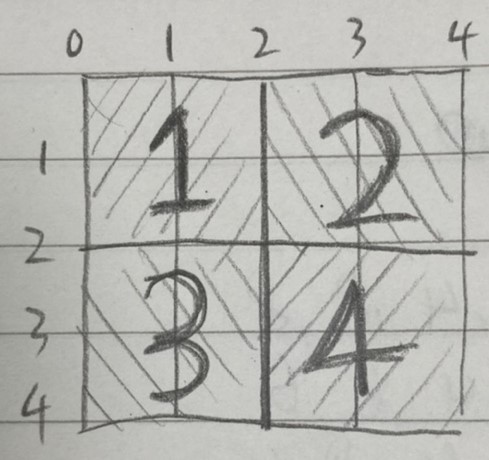
우선 편의상(원래 수학에서 1~4사분면은 저 순서 아니다) 이렇게 1~4사분면으로 나누고, 1사분면부터 생각해보자.
압축을 계속 하다보면 알 수 있겠지만, 점을 찍은 곳의 좌표(x1, y1) = (0, 0)는 변하지 않고 x2, y2만 변한다.
2사분면은 어떨까? 점 찍은 곳의 좌표(x2, y1) = (4, 0)는 변하지 않고 x1, y2만 변한다.
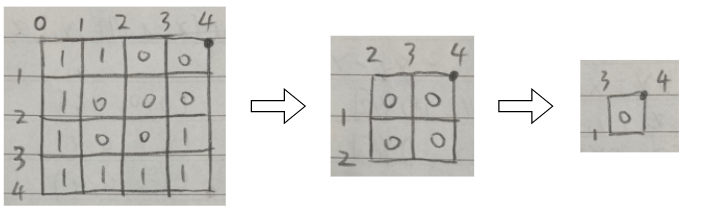
줄어들 때 변하는 좌표의 값은 중간값으로 변한다. 이를 코드로 표현해준다.
1
2
3
4
5
6
7
8
9
def split(x1, y1, x2, y2):
MID_X, MID_Y = x1 + (x2 - x1) // 2, y1 + (y2 - y1) // 2
areas = [
[x1, y1, MID_X, MID_Y],
[MID_X, y1, x2, MID_Y],
[x1, MID_Y, MID_X, y2],
[MID_X, MID_Y, x2, y2]
]
return areas
5. 함수 f() 구현
그리고 어떻게 구성될지는 모르겠지만 배열과 사각형의 범위를 넣어주면 그 범위 안에서 압축도 알아서 하고 아무튼 숫자를 다 체크해서 반환해주는 마법의 함수 f()
그리고 어떻게 구성될지는 모르겠지만 배열과 사각형의 범위를 넣어주면 그 범위 안에서 압축도 알아서 하고 아무튼 숫자를 다 체크해서 반환해주는 마법의 함수 f()의 구현에 대한 대략적인 아이디어는 이렇다.
- 압축 가능한지 체크한다. (크기 1의 사각형까지 쪼개진 경우 압축이 가능한것으로 판단한다.)
- 압축이 안되면 4분할 한다.
- 분할한 구역들별로 전부 다 사각형의 숫자를 세서 result에 더하고 반환한다.
우선 압축이 되는지를 체크해보고 되면 범위 내의 사각형들 중 첫번째 사각형의 숫자를 result에 더하고 result를 반환한다.
1
2
3
4
5
6
7
def f(arr, x1, y1, x2, y2):
result = [0, 0]
compressible = check_if_compressible(arr, x1, y1, x2, y2)
if compressible: # 5-1
result[arr[y1][x1]] += 1
return result
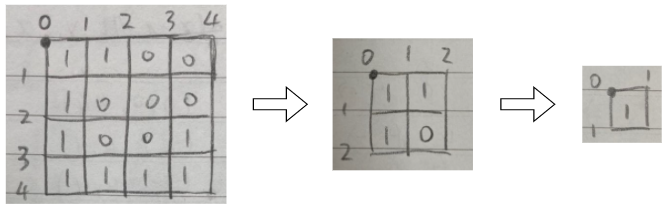
만약 우리가 체크할 사각형이 아래와 같은 사각형만 있다면 이걸로 끝나겠지만 안타깝게도 그렇진 않다.
따라서, 압축이 불가능한 경우는 4분할 해준다.
1
2
3
4
5
6
7
8
9
def f(arr, x1, y1, x2, y2):
result = [0, 0]
compressible = check_if_compressible(arr, x1, y1, x2, y2)
if compressible:
result[arr[y1][x1]] += 1
return result
areas = split(x1, y1, x2, y2) # 5-2
분할한 사분면별로 다시 체크해서 0과 1의 개수를 세온다. 그리고 어떻게 구성될지는 모르겠지만 배열과 사각형의 범위를 넣어주면 그 범위 안에서 압축도 알아서 하고 아무튼 숫자를 다 체크해서 반환해주는 마법의 함수 f()를 사용한다.
(*area는 x1, y1, x2, y2 타이핑 다시 하기 귀찮아서 저렇게 그대로 넣어줬다.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def f(arr, x1, y1, x2, y2):
result = [0, 0]
compressible = check_if_compressible(arr, x1, y1, x2, y2)
if compressible:
result[arr[y1][x1]] += 1
return result
areas = split(x1, y1, x2, y2)
for area in areas: # 5-3
zero, one = f(arr, *area)
result[0] += zero
result[1] += one
return result
Comment
처음에 구현할 때 형태를 보고
- 오 재귀적인 구성?
- 재귀 = 나눈다?
로 생각이 먼저 들어서 나누는거 먼저 구현하다가 테스트 케이스 10번만 자꾸 틀리길래 압축 가능한지를 먼저 체크하도록 로직을 바꾸니 문제가 깔끔하게 해결되었다.
무슨 일이든 역시 서순은 정말 중요한듯..
