Link
Introduction
DFS, BFS 하면 가장 먼저 떠오르는 문제가 미로찾기라고 한다면 백트래킹의 대표적인 문제는 N-Queen 이다.
 모든 엔딩을 보기 위해 모든 선택지를 다 골라본다.
모든 엔딩을 보기 위해 모든 선택지를 다 골라본다.
백트래킹은 검사를 하다가 현재의 선택지가 틀렸다는 걸 알게 되면 그 선택을 취소하고 그 선택지 대신 다른 선택지를 골라가며 탐색한다는 점에서 재미있는 알고리즘이다.

2022 KAKAO BLIND RECRUITMENT 양궁대회에서도 백트래킹을 사용하였는데, 정리해야지 정리해야지 하고 미루다가 이제야 정리를 하게 됐다.
Note
- 같은 그룹 라인에 퀸을 놓지 않아야 한다.
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
answer = 0
def f(x, n, group1, group2, group3):
global answer
if x == n:
answer += 1
return
for y in range(n):
if group1[x-y] or group2[y] or group3[x+y-n+1]:
continue
group1[x-y], group2[y], group3[x+y-n+1] = 1, 1, 1
f(x+1, n, group1, group2, group3)
group1[x-y], group2[y], group3[x+y-n+1] = 0, 0, 0
def solution(n):
global answer
group1 = [0 for _ in range(1 + 2*(n-1))]
group2 = [0 for _ in range(n)]
group3 = [0 for _ in range(1 + 2*(n-1))]
f(0, n, group1, group2, group3)
return answer
1. 퀸의 특성 파악
시작하기에 앞서, 퀸에 대해서 생각해보자.
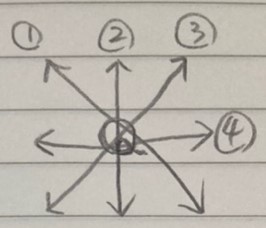
퀸은 그림 처럼 8방향, 4개의 축 안에서 이동이 가능하다. 퀸을 어디에 놓던지, 이 4개의 축 안에 서로의 퀸이 놓이면 안 된다.
퀸을 x방향으로 1개씩 놓아나간다고 하고, 4번의 경우는 제외한 채 1, 2, 3번 라인을 생각해보자.
우선 가장 간단한 2번 라인부터 생각해보자면, y 값이 같지 않으면 된다. n = 4 기준으로 이 y라인 그룹은 4개가 생긴다.
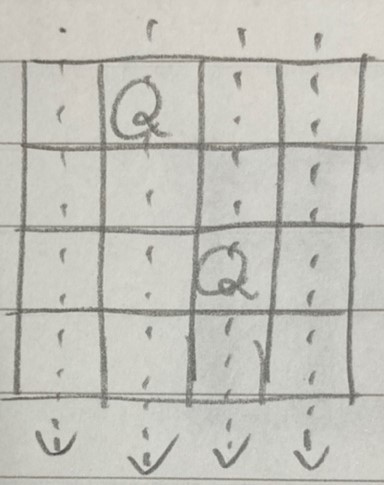
대각선을 살펴보자. 퀸을 (3, 3)에 놓은 아래의 그림을 보면 규칙을 발견할 수 있다.
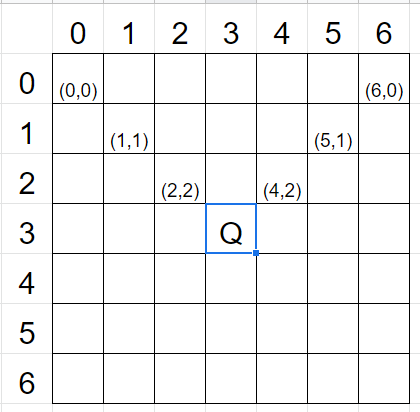
1번 라인은 모두 x-y=0로 값이 같다.
3번 라인의 경우 모두 x+y=n-1를 따르므로, x+y-n+1=0로 값이 모두 같다.
그럼 대각선 라인의 개수는 어떻게 알 수 있을까?
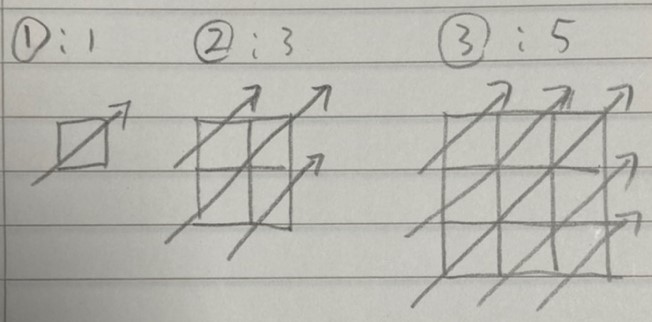
1 + 2*(n-1)개씩 대각선 라인이 늘어난다는 규칙을 발견할 수 있다.
2. solution() 구현

우선 1, 2, 3번 그룹을 각 개수만큼 만들어주자
1
2
3
4
def solution(n):
group1 = [0 for _ in range(1 + 2*(n-1))] # 2-1
group2 = [0 for _ in range(n)] # 2-1
group3 = [0 for _ in range(1 + 2*(n-1))] # 2-1
파이썬에는 포인터가 없어 number 타입의 변수 값을 함수 안에서 수정할 수 없으므로 글로벌 변수 answer를 만들고 f()를 실행하면 answer의 값을 변경할 수 있게 글로벌 변수로 answer를 정의한다.
체크하는 방향은 x방향이고, 0~n 사이를 체크한다.
1
2
3
4
5
6
7
8
9
10
11
12
answer = 0 # 2-2
def f(x, n, group1, group2, group3): # 2-2
pass
def solution(n):
global answer # 2-2
group1 = [0 for _ in range(1 + 2*(n-1))]
group2 = [0 for _ in range(n)]
group3 = [0 for _ in range(1 + 2*(n-1))]
f(0, n, group1, group2, group3) # 2-2
return answer
3. 함수 f() 구현
백트래킹의 기본은 다음과 같다.
- 마지막 선택지에 도달하면(base condition) 결과 값을 기록해둔다.
- 모든 선택지 중 선택할 수 있는(보통은 이미 선택하지 않은) 선택지를 선택 상태로 만들고 재귀호출한다.
- 재귀호출이 끝나면 방금 선택지를 초기화한다.
우선 base condition일 때 결과를 카운트 한다.
1
2
3
4
5
6
7
8
answer = 0
def f(x, n, group1, group2, group3):
global answer
if x == n: # 3-1
answer += 1
return
모든 y축에 있는 칸에 Q를 하나씩 놓아볼 건데, 이미 같은 그룹라인에 퀸이 점유하고 있는 경우는 패스한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
answer = 0
def f(x, n, group1, group2, group3):
global answer
if x == n:
answer += 1
return
for y in range(n):
if group1[x-y] or group2[y] or group3[x+y-n+1]: # 3-2
continue
어딘가에 Q를 놓았다면 Q가 놓인 자리에 해당하는 그룹들은 점유상태로 바꿔주고, 다음 x축의 칸으로 넘어간다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
answer = 0
def f(x, n, group1, group2, group3):
global answer
if x == n:
answer += 1
return
for y in range(n):
if group1[x-y] or group2[y] or group3[x+y-n+1]:
continue
group1[x-y], group2[y], group3[x+y-n+1] = 1, 1, 1 # 3-3
f(x+1, n, group1, group2, group3) # 3-3
해당 선택지를 선택하지 않음 상태로 바꿔준다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
answer = 0
def f(x, n, group1, group2, group3):
global answer
if x == n:
answer += 1
return
for y in range(n):
if group1[x-y] or group2[y] or group3[x+y-n+1]:
continue
group1[x-y], group2[y], group3[x+y-n+1] = 1, 1, 1
f(x+1, n, group1, group2, group3)
group1[x-y], group2[y], group3[x+y-n+1] = 0, 0, 0 # 3-4
4. 조금 더 깔끔한 코드
아래의 코드는 좀 더 깔끔하긴 하지만 직관적이지 못해서 아래의 코드를 채택하지는 않았다.
방식은 비슷한데 글로벌 변수 answer를 사용하지 않는 방법이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def f(x, n, group1, group2, group3):
result = 0
if x == n:
return 1
for y in range(n):
if group1[x-y] or group2[y] or group3[x+y-n+1]:
continue
group1[x-y], group2[y], group3[x+y-n+1] = 1, 1, 1
result += f(x+1, n, group1, group2, group3)
group1[x-y], group2[y], group3[x+y-n+1] = 0, 0, 0
return result
def solution(n):
group1 = [0 for _ in range(1 + 2*(n-1))]
group2 = [0 for _ in range(n)]
group3 = [0 for _ in range(1 + 2*(n-1))]
return f(0, n, group1, group2, group3)
번외. 빌런
세상에…
Comment
백트래킹을 처음 접할 때의 혼란함은 재귀함수를 처음 접했을 때와 비슷했던 것 같다. 개념 자체는 어렵지 않지만 구현이 좀 헷갈리는 케이스.
