Link
Introduction
이전의 연산 결과를 기억하면서 그 결과를 가지고 연산을 계속해나간다는 DP(다이나믹 프로그래밍)의 개념을 이해 못해서 굉장히 고생했었던 기억이 있다.
아무래도 처음 접했던 DP 문제들이 너무 난이도가 높아서 DP 자체에 집중하여 학습하기 보다는 문제가 주는 복잡함에 압도되어서 정신이 없어서 그랬던 것 같다.
이 문제는 간단하면서도 전형적인 DP 문제로 DP의 개념을 익히는데 좋을 입문용 문제라고 생각한다.
Note
- 연속으로 같은 열을 밟을 수 없다는 규칙에 주의
Solution
1
2
3
4
5
6
7
8
def solution(land):
for row in range(1, len(land)):
prev_row = land[row-1]
land[row][0] += max(prev_row[1], prev_row[2], prev_row[3])
land[row][1] += max(prev_row[0], prev_row[2], prev_row[3])
land[row][2] += max(prev_row[0], prev_row[1], prev_row[3])
land[row][3] += max(prev_row[0], prev_row[1], prev_row[2])
return max(land[-1])
1. 어떻게 이동해 나갈 것인가
시작점에서 출발해 모든 경우를 고려하는 것도 문제를 해결할 수 있는 방법이겠지만, 더 효율적인 방법이 있다. 바로 점수의 합계가 최고점이 될 수 있는 경우만 고민하며 전진하는 것이다.
한 칸 전진한 후가 가장 최고점인 경우만 고려하면서 가보자.
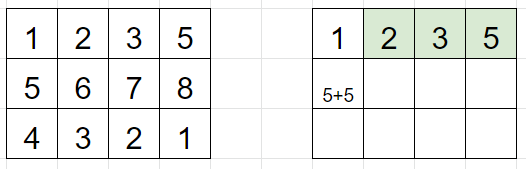
우선 두 번째 행의. 두 번째 행의 첫 번째 열의 값이 최대값이 되기 위해서는 그 이전 열에서 가장 큰 점수와 현재 점수를 더한 점수여야 한다. 이 때 같은 열은 두 번 연속으로 못 밟으므로 첫 번째 열은 후보에서 제외하고 생각한다.
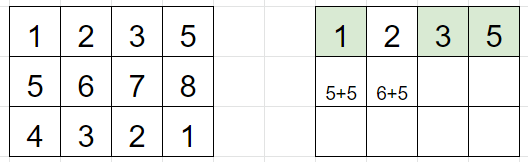
두번째 행도 마찬가지로 현재 점수와 이전 열에서의 최대값을 더한게 최대값이다.
1
2
3
4
5
6
7
def solution(land):
row = 1
prev_row = land[row - 1]
land[row][0] += max(prev_row[1], prev_row[2], prev_row[3])
land[row][1] += max(prev_row[0], prev_row[2], prev_row[3])
land[row][2] += max(prev_row[0], prev_row[1], prev_row[3])
land[row][3] += max(prev_row[0], prev_row[1], prev_row[2])
이렇게 모든 열을 최대 점수를 구하고,
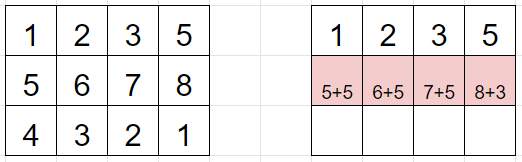
1
2
3
4
5
6
7
def solution(land):
for row in range(1, len(land)):
prev_row = land[row-1]
land[row][0] += max(prev_row[1], prev_row[2], prev_row[3])
land[row][1] += max(prev_row[0], prev_row[2], prev_row[3])
land[row][2] += max(prev_row[0], prev_row[1], prev_row[3])
land[row][3] += max(prev_row[0], prev_row[1], prev_row[2])
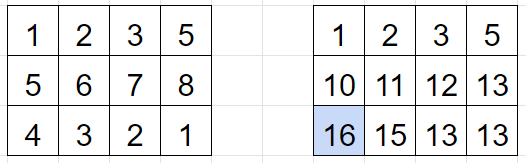
두 번째 행부터 마지막 행까지 모든 최고점수를 구한다.
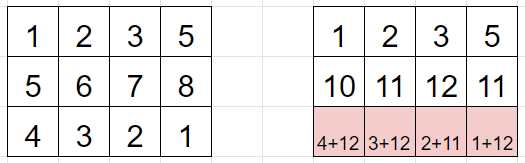
그러면 가장 마지막 행에서 가장 큰 값이 최고점이다.
1
2
3
4
5
6
7
8
def solution(land):
for row in range(1, len(land)):
prev_row = land[row-1]
land[row][0] += max(prev_row[1], prev_row[2], prev_row[3])
land[row][1] += max(prev_row[0], prev_row[2], prev_row[3])
land[row][2] += max(prev_row[0], prev_row[1], prev_row[3])
land[row][3] += max(prev_row[0], prev_row[1], prev_row[2])
return max(land[-1])
Comment
때로는 시작점부터 하나의 길을 따라 문제를 해결해 나가는 방법이 아니라 최적의 결과값을 가지는 중간지점을 계속해서 갱신해나가는 방법이 더 간단하고 빠르게 문제를 해결하는 경우가 있다.
머리로는 알고 있는데 가끔 이걸 떠올리지 못해 괜히 헤매는 경우가 많아서 문제지만..
