Introduction
Dynamic Programming은 알고리즘 중에서도 딱 하나로 정의가 되지 않는 알고리즘이다.
DP와 관련된 내용을 인터넷에서 찾아보면 대부분 어딘가에서 가져와서 돌려쓰는 내용 복붙이 많다. (피보나치 멈춰!)
DP를 쓰려면 점화식을 세워야 한단다.
“음 그럼 점화식은 어떻게 세우죠? 어떤 규칙이 있나요?”라는 물음에,
“이런건 감이다. 익숙해져야 한다. 많이 풀다 보면 패턴이 보인다.”라고 하는 알쏭달쏭한 답만 얻을 수 있었다.
(많은 경우 풀이 방법만 있고, 어떻게 그런 결론을 도출하게 되었는지의 과정에 대한 내 작은 두뇌로도 이해할 만큼의 자세한 설명이 없었다.)
 감이 잘 안 옵니다
감이 잘 안 옵니다
DP에 대해서 공부하면 공부할수록 저 말이 무슨 말인지 이해가 가는 한 편 진리는 언제나 심플하다고 믿는 나로서는 완벽하게 납득이 가진 않았다.
그래서 나도 내 방식대로 정리해봤다.
그래서 DP가 뭔데?
DP(Dynamic Programming)는 고안자인 벨만이 Dynamic이라는 단어가 멋있어서 이름을 저렇게 지었다고 한다.
근데 다들 이 DP를 기억하며 풀기로 바꿔 말하는 것에 대해 동의하는 이유는 DP의 풀이방식에 대한 특징 때문이다.
중복된 하위 문제 (Overlapping Subproblems)
DP는 복잡한 문제를 풀 수 있는 작은 문제로 분할하여 각각을 해결한 뒤 합치는 분할정복(Divide and Conquer) 알고리즘과 비슷하다.
다른 점이 있다면 분할한 작은 문제를 해결한 뒤 그 결과를 저장하고, 다음 단계의 문제를 해결할 때 이전에 해결했던 그 결과값도 같이 이용해서 문제를 해결해 나간다.
1
2
3
4
5
6
7
8
9
10
11
12
13
arr = [1, 2, 3, 4], 0 <= k < len(arr) 일 때,
a[0]부터 a[k]까지의 부분합을 구하라는 문제가 있다고 가정해보자.
위 문제를 단순하게 풀면
sum(a[0:1]) = a[0] = 1
sum(a[0:2]) = a[0] + a[1] = 3
sum(a[0:3]) = a[0] + a[1] + a[2] = 6
sum(a[0:4]) = a[0] + a[1] + a[2] + a[3] = 10 가 되는데,
sum(a[0:4])의 경우, a[0] + a[1] + a[2]까지는 이미 sum(a[0:3])에서 구했기 때문에 굳이 저렇게 길게 쓰지 않아도 앞서 구한 결과 값인 k = 2일 때 값인 6을 이용할 수 있다.
sum(a[0:4]) = 6 + a[3] = 10
즉, 중복된 부분은 이미 전 단계에서 구해놨으니까 같은 거 반복하지 말고 그냥 그거 쓰자는 말이다.
최적 부분 구조 (Optimal Substructure)
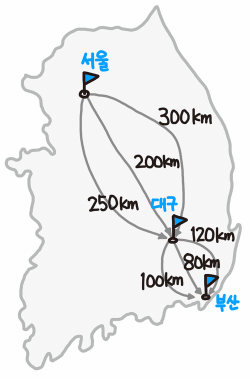
최적 부분 구조는 위의 그림을 보면 단번에 이해 된다.
서울에서 부산까지 가기 위해 중간에 대구를 거칠 때 굳이 300km나 250km가 걸리는 길을 선택하지 않고, 가장 빠른 최적인 200km의 길을 선택하고 또 대구에서 부산까지 80km의 가장 최적의 길을 선택하는 것. 이것이 최적 부분 구조이다.
부분 부분마다 최적의 값을 선택한다는 이야기다.
어떻게 적용하는가?
DP는 Tabulation이라고 하는 방식으로 최적의 값을 저장해 나간다.
보통 1차원 배열과, 2차원 배열을 사용한다.
1차원 배열 - 저장하는 값이 1개
2차원 배열 - 저장하는 값이 2개 이상
References
- https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95
- https://namu.wiki/w/%EA%B7%B8%EB%A6%AC%EB%94%94%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98#s-2.1