Bitwise Operation & Bitmask

Introduction

일반적인 코딩은 사람이 읽을 수 있는 스토리가 담긴 대화지만, 비트 연산(Bitwise Operation)은 컴퓨터와의 대화에 가깝다.

프로그래머는 컴퓨터와도 대화를 할 수 있어야 하는 직업임에도 불구하고 나는 비트 연산의 응용에 약해서 이번 기회에 정리해두기로 했다.

Bitwise Operation

아무래도 컴퓨터가 다루는 이진수의 비트를 직접 조절하기 때문에 비트 연산은 속도가 굉장히 빠르다.

  
int remainder = value % divisor

나눗셈에서 divisor(나누는 수; 제수)가 2의 n승인 경우 divisor-1과 AND 연산자(&)를 통해 나머지를 구할 수 있는데, 이를 이용해 일반 연산과 비트 연산의 속도차이를 측정할 수 있다.

  
// 아래의 두 연산은 같은 결과값이 나온다.
int remainder = value % 1024;
int remainder = value & 0x3FF; // 0x3FF = 1024 - 1 = 1023

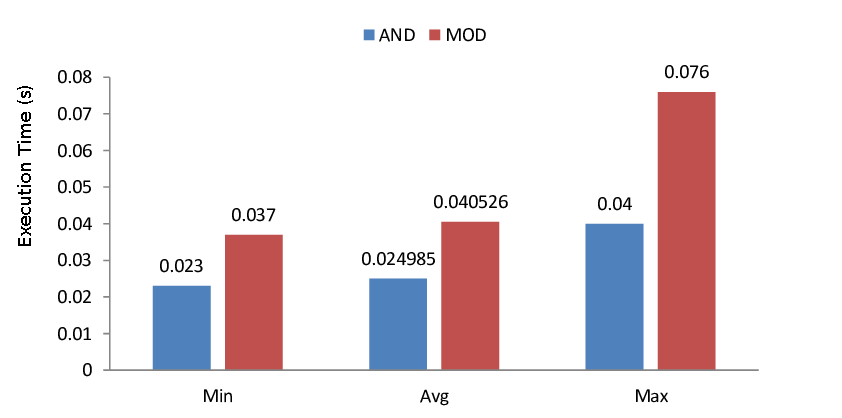MOD vs AND % 연산과 & 연산의 수행시간 차이 by Marco Ziccardi

두 연산의 수행속도는 위의 그래프와 같이 약 2배 가량 차이가 나는데, 이는 엄청난 차이이다.

Bitmask

비트 연산이 속도가 빠르다는건 알겠는데, 보통 어떤 때에 쓰이는걸까?

Bitwise는 주로 Bitmask의 형태로 사용이 된다.

Bitmask는 쉽게 말해 숫자를 이진수로 바꿨을 때 나오는 각각의 비트를 0을 off 상태, 1을 on 상태로 보고 이를 스위치처럼 껐다켰다 하면서 정보를 저장하는 형태를 말한다.

예를 들어, 숫자 8의 경우 이진수 1000(2)로 표현할 수 있는데, 이는 스위치 4개를 가지고 있으면서 1번째 스위치 하나만 켜지고 나머지 3개의 스위치가 꺼졌다고 보면 된다.

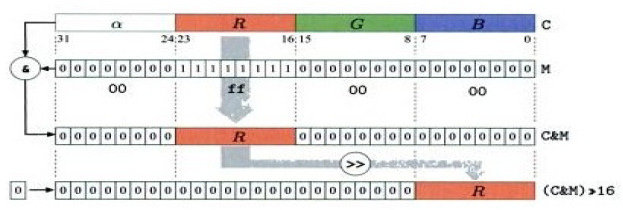RGB Bitmask Bitmask를 이용하여 RGB 값을 저장 및 추출

이를 통해 최대한 지연시간이 적어야 하면서 실시간으로 엄청나게 많은 연산이 필요한 모니터의 RGB 색상값을 표현한다.

SDL 2.0 SDL 2.0 키보드의 키코드 헤더 파일

또 다른 경우로는 동시에 입력값을 기억하고 처리해야 하는 키보드 조합키(modifier), 조이패드 버튼 키코드 등에 Bitmask를 사용한다.

Basic Operation

AND 연산 (&)

대응하는 숫자가 전부 1일 경우 1을 반환

  
int a = 237;   // 11101101
int b = 221;   // 11011101
int c = a & b; // 11001101

OR 연산 (|)

대응하는 숫자 중 하나라도 1일 때 1을 반환

  
int a = 237;   // 11101101
int b = 221;   // 11011101
int c = a | b; // 11111101

XOR 연산 (^)

대응하는 숫자가 다를 경우 1을 반환

  
int a = 237;   // 11101101
int b = 221;   // 11011101
int c = a ^ b; //   110000

NOT 연산 (~)

비트를 반전시킴
- 주의: 파이썬에서는 integer가 signed integer로 동작하는데, 이 연산 후에 bin() 함수 등으로 숫자를 표기하면 값이 생각했던거랑 다르게 찍힌다. (연산은 잘 된다. 표기만 좀 다르게 나올 뿐이지) [참고: Bitwise Operators in Python]
  - 예) ~0b10101001 -> -0b10101000
- 주의: OR연산과 NOT연산은 같이 쓰지 말 것.
  - OR연산을 하기 위해 4 = 100(2)같이 비트가 하나만 있고 나머지는 다 0으로 채워진 숫자에서 3 = 011(2)를 만들고 싶다면 비트를 반전시킬게 아니라 100(2)에서 1을 빼주자.
  - 4 = 100(2)의 비트를 반전시키면 3 = 011(2)이 아니라 -5가 되어서 OR 연산 시에 마이너스 부호의 비트까지 들어가 버린다. 참고: The meaning of Bit-wise NOT in Python (링크는 python에 대한 설명이지만 C++도 Java도 동일하다. 아마 모든 언어가 다 그럴듯.)

  
int a = 237; // 11101101
int c = ~a;  // 00010010

SHIFT 연산 («, »)

비트를 한 칸씩 민다. <<로 밀 경우 가장 오른쪽에 0을 채우고, >>로 밀 경우 가장 오른쪽 비트는 유실된다.
- << 연산의 경우 *2연산과 같고, >>의 경우 /2연산과 같다.

  
int a, b, c;
a = 237;    //  11101101

b = a << 1; // 111011010
b = a * 2;  // 111011010

c = a >> 2  //    111011
c = a / 4   //    111011

Operation Techniques

비트 조회

n번째 비트가 1인지 아닌지를 조회(결과 값이 0이면 없고, 1 이상이면 있는 것)

  
int n = 3;

int a = 233;           // 11101001
int c = a & (1 << n);  //     1000

비트 설정

n번째 비트에 1을 설정

  
int n = 2;

int a = 233;            // 11101001
int c = a | (1 << n);   // 11101101

비트 제거

n번째 비트의 1을 제거

  
int n = 3;

int a = 233;            // 11101001
int c = a & ~(1 << n);  // 11100001

비트 토글

n번째 비트를 뒤집는다.

  
int n = 2;

int a = 233;           // 11101001
int c = a ^ (1 << n);  // 11101101

Advanced Techniques

가장 오른쪽의 0 위치 획득

  
int a = 233;          // 11101001
int c = (a+1) & ~(a); //       10

가장 오른쪽에 설정된 1 위치 획득

  
int a = 232;        // 11101000
int c = a & ~(a-1); //     1000

가장 오른쪽에 설정된 1 제거

  
int a = 232;       // 11101000
int c = a & (a-1); // 11100000

Comment

예전부터 정리해야지 해야지 해놓고 이제야 정리를 하게 됐다..비트 조작은 익숙해지면 강력한 도구이지만, 너무 어렵기도 하고 가독성이 별로 좋지 않아 사용에 주의가 필요하다.

일단 뼈대만 만들고 내용을 추후에 조금씩 더 추가할 예정이다.