Link
Introduction
프로그래밍에서 가장 중요한 부분은 해결해야 할 문제를 나누어서 생각하는 것이다.
아직도 많이 서툰 부분이긴 하지만, 이게 잘 안될 때는 한꺼번에 너무 많은 것들을 동시에 고민하다보니 머리속에서 꼬여서 문제 해결이 너무 힘들었던 경우가 있었다.
이번 문제 해결에서는 단위 정사각형을 만들고 그 단위 정사각형을 기준으로 체크해 나가며 규칙을 파악한 뒤 문제 풀이에 적용한다.
Note
- 2X2의 단위 정사각형을 먼저 생각해보고, 이를 움직이며 체크해 나간다.
Solution
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def solution(board):
if len(board) == 1:
return max(board[0])
answer = 0
for i in range(1, len(board)):
for j in range(1, len(board[0])):
if board[i][j] == 1:
board[i][j] = 1 + min(board[i-1][j-1], board[i][j-1], board[i-1][j])
answer = max(answer, board[i][j])
if answer == 0:
for i in range(len(board)):
answer = max(answer, board[i][0])
return answer ** 2
풀이
1. 단위 정사각형 체크
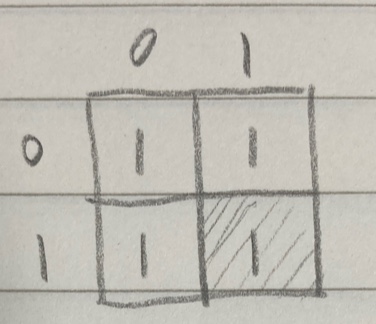
우선 아래와 같은 정사각형들을 생각해보자. 이 정사각형(2X2)들은 앞으로 체크해나갈 기본 단위 사각형이다.
이 단위 정사각형의 한 변의 길이가 2가 되는 기준은 모든 작은 사각형의 숫자가 1일 때이다. (하나라도 0이 섞여 있을 경우 단위 정사각형을 만들 수 없으므로)
이걸 체크하는 방법은 색칠되어 있는 칸(x,y)을 기준으로 왼쪽(x-1, y), 위쪽(x, y-1), 왼쪽 위(x-1, y-1) 3방향의 사각형의 숫자가 모두 1인지 아닌지를 체크 하는 것이다.
이걸 코드로 구현해보자. 보편적인 체크를 위해 (1,1) 위치에서부터 체크해 나간다. (위에서 그린 사각형의 색칠한 부분)
1
2
3
4
5
6
7
8
def solution(board):
for y in range(1, len(board)):
for x in range(1, len(board[0])):
if board[y][x] == 1:
# 아래의 3개의 값이 1인지 체크만 하면 된다.
board[y][x-1] # 왼쪽
board[y-1][x] # 위쪽
board[y-1][x-1] # 왼쪽 위
2. 지뢰찾기
체크하는 건 끝났으니 실제로 넓이를 구해보기 전에 우선 아래의 단위 사각형에 대해 생각해보자.
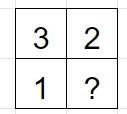
? 안에 들어갈 숫자는 무엇일까?
이를 알아보기 위해 주어진 사각형을 단위 사각형 별로 체크하며 확장시켜 나가보자.
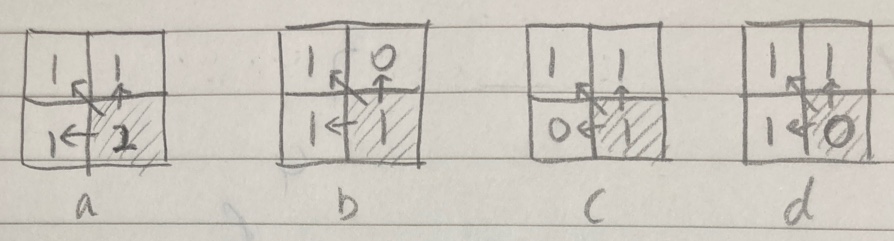
우선 진하게 색칠된 사각형을 기준으로, 이 사각형의 숫자가 1이기 위해서는 왼쪽과 왼쪽위 사각형의 숫자가 몇이어야 할까?
어느쪽이든 하나는 값이 0이어야 한다. 둘 다 1 이상이면 단위 사각형이 완성되어버려 진하게 칠해진 숫자가 2가 될 수 밖에 없기 때문이다.
또한, 숫자가 3인 사각형 옆의 사각형은 무조건 1 이상이다. 그렇지 않으면 단위 사각형이 완성되지 않기 때문이다. 따라서 위 그림과 같이 1과 0을 적어둔다.
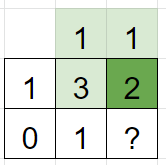
다음은 숫자가 2인 사각형을 보자. 이 사각형은 알기 쉽다. 3방향(왼쪽, 위쪽, 왼쪽위) 모두 숫자가 1 이상이면 된다. 일단 1로 적어두고 다음으로 넘어간다.
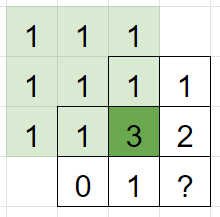
이번에는 숫자가 3인 사각형을 체크해보자. 숫자가 3이기 위해서는 옅게 칠해진 모든 부분의 숫자가 1 이상이어야 한다. 따라서 우선은 1을 전부 채워둔다.
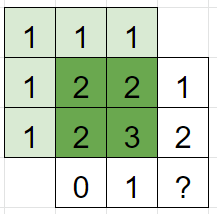
다시 체크해보니 숫자가 모두 1은 아니다. 숫자가 2이어야 하는 부분은 숫자를 갱신해준다.
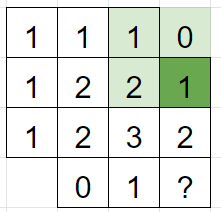
진하게 색칠된 부분의 넓이가 1이기 위해서는 위쪽 사각형의 숫자가 0이어야 한다.
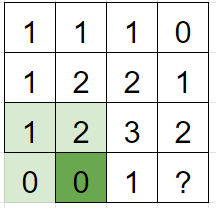
마지막으로 남은 부분을 채워준다. 진하게 색칠된 부분의 숫자가 0이려면 바로 옆에 있는 사각형의 숫자도 0이어야 한다.
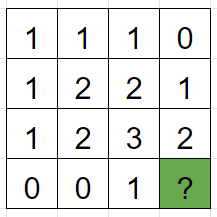
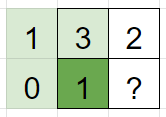
표를 완성해놓고보니 규칙을 발견할 수 있다. 어떤 사각형의 숫자가 1 이상이라면 그 숫자는 3방향(왼쪽, 위쪽, 왼쪽위)의 사각형들의 숫자 중 가장 작은 것 + 1이라는 점이다. 따라서 ?에 들어갈 숫자는 2이다.
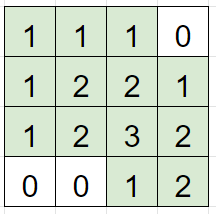
그리고 표에서 숫자가 1 이상인 사각형들을 다 칠해보면 더 명확하게 알 수 있다.
이 사실을 참고하여 숫자를 갱신하는 부분을 코드로 구현해 보자.
1
2
3
4
5
6
def solution(board):
for y in range(1, len(board)):
for x in range(1, len(board[0])):
if board[y][x] == 1:
board[y][x] = 1 + min(board[y][x-1], board[y-1][x], board[y-1][x-1]) # 2
3. 최대 넓이 구하기
아까 그 값들 중 숫자가 큰 값이 가장 큰 정사각형의 한 변의 길이이므로, 이를 저장해 두었다가 제곱한 값을 반환한다.
1
2
3
4
5
6
7
8
def solution(board):
answer = 0
for y in range(1, len(board)):
for x in range(1, len(board[0])):
if board[y][x] == 1:
board[y][x] = 1 + min(board[y][x-1], board[y-1][x], board[y-1][x-1])
answer = max(answer, board[y][x]) # 3
return answer ** 2
4. 코너 케이스
단위 정사각형이 2X2 사각형이기에 위 풀이에는 한 가지 고려하지 않은 것이 있다. 바로 아래와 같은 케이스이다.
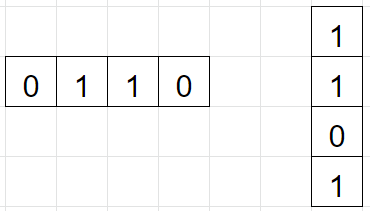
이 케이스를 고려하여 코드에 반영한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def solution(board):
if len(board) == 1: # 그림의 왼쪽 케이스
return max(board[0])
answer = 0
for y in range(1, len(board)):
for x in range(1, len(board[0])):
if board[y][x] == 1:
board[y][x] = 1 + min(board[y][x-1], board[y-1][x], board[y-1][x-1])
answer = max(answer, board[y][x])
if answer == 0: # 그림의 오른쪽 케이스
for i in range(len(board)):
answer = max(answer, board[i][0])
return answer ** 2
Comment
일일이 표 만들고 편집하느라 푸는 시간보다 정리하는 시간이 훨씬 더 많이 걸렸다. 그래도 만들어 놓고 보니 뭔가 뿌듯…
